7 Directed Acyclic DAG (DAG)

This lecture introduces Directed Acyclic Graphs (DAG) and their properties, including cycle detection and topological sorting.

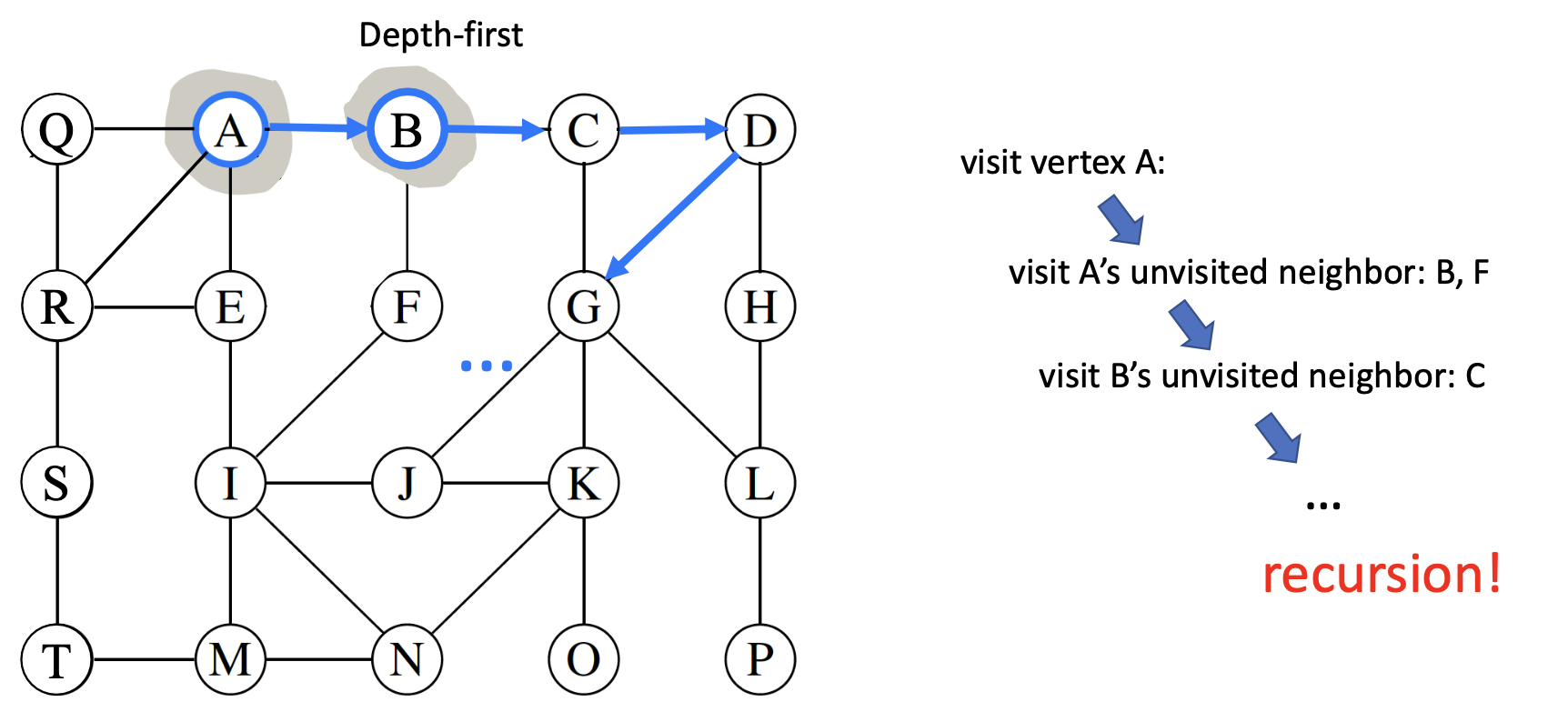
DAG and DFS recap

Figure 1: DFS

Cycle Detection

Algorithm cycleDetection(u, ancestors):
    for each of u's outgoing edges, e=(u,v), do {
        if v is among ancestors, return true
        if vertex v has not been visited, then {
            record vertex v and its discovery edge e
            add v to ancestors
            if cycleDetection(v, ancestors) return true
            remove v from ancestors
        }
    }

Topological Sort

Definition 1 A topological ordering of a graph is an ordering \(v_1,\dots,v_n\) of the vertices of the graph such that for every edge \((v_i,v_j)\) in the graph, it must be that \(i<j\). - That is, any edge is always from a higher-ranked vertex to a lower-ranked one.

• Claim: A DAG always has topological ordering.
  • A DAG always has at least one “source” vertex (that is, a vertex with no incoming edges).
  • Hence, we can give highest rank to this source vertex.
  • Since the remaining subgraph is still a DAG, we still have a source vertex in it for which we can give the next highest rank, and so on.
  • Repeat this process until all vertices are ranked. This gives a topological ordering.